 “Deus joga dados com o Universo, mas os dados são ‘viciados’ – o principal objetivo da Física é descobrir as regras segundo as quais… tal fato aconteceu.” (Joseph Ford)
“Deus joga dados com o Universo, mas os dados são ‘viciados’ – o principal objetivo da Física é descobrir as regras segundo as quais… tal fato aconteceu.” (Joseph Ford)
1) Probabilidade… a teoria formal
Para nós seria muito vantajosa a capacidade de prever – de modo fidedigno… – o que vai acontecer no futuro…Em certos casos muito excepcionais – podemos até prever o futuro, como tendo um, e apenas um resultado — o que acontece, por exemplo…ao prevermos a posição de um planeta…a partir da sua condição presente (inicial), por leis dinâmicas do movimento. Mas, na maioria dos casos, só temos ‘vaga ideia’ do que o futuro nos reserva.
Todavia, de um conjunto de resultados possíveis…existe um conjunto especial de casos em que, apesar de não podemos dizer com segurança qual resultado irá ocorrer – podemos ter um conhecimento fidedigno da proporção com que esses resultados ocorrerão num grande número repetido de situações semelhantes. – Por exemplo, quem lança 2 dados não sabe o que trará o próximo lançamento…mas sabe que numa longa série de lançamentos…a soma do resultado 7 irá surgir, aproximadamente…uma vez… – a cada 6 lançamentos efetuados.
obs. a probabilidade da soma 7, para 2 dados, com 6 faces cada um, é o total de variações 6×6=36… dividido pelo total de possibilidades (1+6),(2+5),(3+4),(4+3),(5+2),(6+1)=6; a probabilidade é 6/36=1/6
Definindo-se uma coleção de resultados básicos, por exemplo… – o número de resultados possíveis desses 2 dados, atribui-se números entre 0 e 1 à sub-coleções desse tal conjunto. Assim, 1/6 corresponde, exatamente, à possibilidade que consiste…em “sair o número 7”. À coleção caracterizada por “sair um número par” atribuímos o número 1/2. Ao resultado ‘vazio‘ (não ocorrer nenhum dos resultados possíveis) é dada uma probabilidade 0… e, ao resultado trivial (ocorrer qualquer dos resultados possíveis), é dada uma probabilidade 1. A investigação de tais situações — começando com a típica situação de jogo … resultou no desenvolvimento da “teoria das probabilidades“. – Da frequência com que se poderia esperar a ocorrência de determinado resultado, num grande número de idênticas jogadas repetidas, construiu-se um ‘formalismo‘…que, embora conhecidas suas ideias básicas há centenas de anos, na realidade, só se estabeleceu como teoria, nos anos 30…do século 20.
Seu postulado mais importante é o da aditividade. Suponhamos que… um resultado na coleção A, não possa estar na coleção B, e vice-versa. Sendo assim, a ‘probabilidade’ atribuída ao resultado “A ou B” é a soma das probabilidades…atribuídas a A… e a B.
Desse modo, se não podemos ser simultaneamente ‘flamenguistas’ e ‘tricolores’… – a probabilidade de sermos de uma das torcidas ‘Fla/Flu‘, é a soma da ‘probabilidade’ de sermos… “tricolores”… — com a restante ‘probabilidade’ de sermos “flamenguistas”.
Em circunstâncias comuns, estamos familiarizados com a situação em que o número de resultados básicos possíveis é finito…o dado com 6 faces… – a roleta com 37 casas…e, assim por diante. No entanto, o matemático, e como veremos, o físico, têm de lidar com casos, em que o número de ‘resultados básicos‘ é infinito. Por exemplo, uma partícula pontual com qualquer uma … de um número infinito de ‘posições’ possíveis numa caixa. Para isso então, pressupõe-se uma “aditividade contável”; pressuposto natural, mas com algumas ‘consequências peculiares‘. – Uma delas é que a probabilidade 0 já não é atribuída apenas ao ‘conjunto vazio’…em que não ocorre qualquer consequência básica; passando também a ser atribuída a…”conjuntos não vazios”. Por exemplo…se o jogo no qual estamos envolvidos consiste em escolher um nº entre todos ‘números reais‘…de 0 a 1… – a ideia de “aditividade contável” implica que…a probabilidade de se obter um ‘número racional‘ … (que pode ser representado como uma fração de 2 nºs inteiros), é zero, mesmo existindo um nº infinito desses números (inteiros) racionais na coleção.
Outra noção importante na teoria é a de ‘probabilidade condicional‘. – Supondo sabermos que saiu um 7 no lançamento de 2 dados… qual a probabilidade, dado esse resultado, de num dos dados ter saído o 1? … Bem, a soma 7 pode sair de 6 maneiras, mas só em 2 dos casos é que em um dos dados sai 1. Por isso… a probabilidade é 1/3.
A frequência prevista de um tipo de resultado B, dada a ocorrência de um tipo de resultado A… é a probabilidade de B – sob a condição de A; ou… a probabilidade condicional de B em relação a A. Mas, se a probabilidade de B em relação a A for “incondicional“… – assim como a probabilidade de A, não depender da de B… pode-se dizer que A e B são “probabilisticamente independentes entre si“.
Considera-se… ‘habitualmente’… que 2 lançamentos sucessivos de uma moeda são independentes. Assim, a probabilidade de sair cara no segundo lançamento continua a ser 1/2… ou seja, o resultado do primeiro lançamento…é irrelevante… para esta probabilidade.
No entanto — as probabilidades de uma pessoa ser pernambucana…e, do nordeste do país… – não são, certamente, independentes. A probabilidade de ser pernambucano – dado ser do nordeste do país… é, certamente mais elevada que a probabilidade desta pessoa ser pernambucana … devido a ser brasileira.
‘leis dos grandes números’ “O que me parece verdadeiramente crucial na ciência, é a descoberta de princípios subjacentes…conectando, de alguma forma…fenômenos naturais” (Paul Davies)
Pode-se demonstrar, a partir dos postulados básicos da ‘teoria das probabilidades‘ – um grupo importante de teoremas conhecido por “leis dos grandes números”… Será que, em um número reduzido de lançamentos de uma moeda é de se esperar que saiam ‘caras’ metade das vezes?… – Se o número de lançamentos for ímpar … isso não pode acontecer. Mas, mesmo que o número de lançamentos seja par…é de se esperar que o resultado real divirja da proporção exata de 1/2 – dada qualquer sequência de lançamentos… Porém, à medida que o número de lançamentos se tornar muito elevado… — pode-se esperar uma convergência da frequência dos resultados ‘caras‘… – à probabilidade postulada de 1/2.
Em suma, o que a “lei dos grandes números” nos diz, é que a probabilidade de uma tal convergência aproxima-se de 1 (certeza probabilística), à medida que o número de lançamentos tende a infinito…para lances probabilisticamente independentes entre si. Assim, embora não possamos demonstrar que… – ‘em qualquer sequência de jogadas, tendendo a infinito…a frequência probabilística convergirá’… – podemos demonstrar, que…por meio de ‘lances independentes‘… tal resultado é uma ‘certeza probabilística’.
Uma coisa… é termos um conjunto de axiomas formais probabilísticos, exibindo algumas variações, sem levantar problemas de compreensão; outra, muito diferente, é concordarmos sobre o que é…”probabilidade”.
2) Interpretações objetivas da ‘probabilidade‘ Do que estamos falando quando falamos sobre probabilidades?…Dada a conexão íntima entre frequências de resultados…e atribuições de probabilidade… não seria mais simples identificar…”probabilidades”… – com “frequências relativas…e efetivas de ocorrências”?
Para acomodar os casos em que o número de resultados básicos não é finito… mas infinito, poderíamos querer generalizar… — e falar de ‘proporções efetivas‘…em vez de ‘frequências efetivas‘ … mas, a ideia básica seria a mesma. Contudo…esta ‘perspectiva simples’ enfrenta a trivial objeção, de que… “não se espera que, em qualquer classe efetiva de eventos, as frequências, ou proporções efetivas sejam as probabilidades exatas”… É de se esperar, um certo tipo de centralização dos resultados efetivos, nos valores da probabilidade – mas não, a sua identidade (‘desvio padrão’=O).
Sugere-se então, que deveríamos identificar as probabilidades … com frequências a longo prazo… – isto é, à medida que o número de lances tende a infinito… – Um dos problemas desta perspectiva porém…é que, obviamente, o nº efetivo de lances é sempre finito…Mas, o que seria então, esta peculiar…e ideal sequência de experiências, que ‘tendem a infinito’ – na qual deverão se determinar as frequências?… – Será supostamente…algo efetivo, ou antes, uma espécie de idealização?… – E, neste último caso… o que aconteceria então… à “perspectiva original”… – de probabilidades como frequências… ou, proporções efetivas?
Uma outra dificuldade dessa perspectiva é que, até a longo prazo, a conexão entre frequências e probabilidades – é meramente estatística…Na verdade, as ‘leis dos grandes números‘ só são válidas…quando as experiências independem entre si; e…isso é uma noção probabilística. Pior ainda, a identidade entre frequência e probabilidade, mesmo a longo prazo…só é assegurada com probabilidade 1, o que não significa… – em uma aleatória sequência infinita de lances…que os limites da frequência e probabilidade relativas…tenham obrigatoriedade de serem idênticos.
Desse modo…a “probabilidade” seria uma espécie de “proporção simples“, representando a estrutura do mundo, ao nível das generalizações fundamentais.
Outra interpretação pertinente da probabilidade olha antes, para o processo pelo qual as frequências exigidas seriam geradas. A probabilidade…de acordo com esta perspectiva, é uma característica do objeto, ou do processo que envolve um objeto – em função da qual um resultado pode ser produzido, ou não…Descrever como (1/2) a probabilidade de sair ‘caras’ no lançamento de uma moeda – é atribuir ao equipamento de lançamento… ou, à situação/ocasião, uma propensão para gerar caras metade das vezes…caso se tente fazer um número elevado de lançamentos. A probabilidade, por esta perspectiva, é o atributo de um lançamento (sua “disposição” para originar o resultado de um gênero específico).
O objetivo de todas estas interpretações é atribuir probabilidades ao resultado de uma classe de experiências – quer seja a frequência, ou proporção desse resultado…uma projeção ou idealização do mesmo.
Determinar o “grau de probabilidade” inerente a um acontecimento único, ao invés de ser apenas medida de uma classe de resultados com respeito a certa classe de acontecimentos, envolve bem mais que questões puramente filosóficas – abrange questões como…saber se a ‘perspectiva disposicional’ pressupõe uma “base de apoio frequencial“…e ainda, se essa “perspectiva” pode resolver dificuldades encontradas em outros setores… – E, além disso, questões físicas também serão levantadas – pois…saber se as proporções que observamos no mundo são…num sentido irredutível…inerentes a acontecimentos únicos, se relaciona intimamente com a questão de saber se há… em todos eventos, condições suficientes, que determinem, exatamente, que só um…dos resultados possíveis…irá efetivamente ocorrer.
Mas, será que pode haver casos em que subsista uma multiplicidade de resultados… – ainda que se especifiquem todas as condições conhecidas, desconhecidas…ou mesmo impossíveis de serem conhecidas, que regulam o acontecimento? Esta é uma importante questão na ‘mecânica quântica’.
3) Aleatoriedade
Outra área a ser explorada por quem deseje entender probabilidade como característica objetiva do mundo trata-se do problema da ‘aleatoriedade‘, cujas características podem se dividir em 2 tipos distintos…a) subjetiva: não se conhecem suas causas, mas existem fórmulas as explicando; exemplo: imagens fractais… — estudadas pela…”matemática”. b) objetiva: causas inexistentes puramente “aleatórias”, sempre de modo diferenciado, sem jamais repetir suas “ações anteriores“.
Por exemplo o ‘movimento Browniano‘ aleatório de partículas macroscópicas num fluído, como consequência dos choques dessas moléculas…com as partículas… – Objetivamente, este estudo levou a resultados interessantes – ainda que não completamente conclusivos. Uma boa proposta para explicar a ‘aleatoriedade objetiva’ apoia-se na intuição de que, na coleção de todas sequências…aquelas ordenadas deveriam ser raras; noção que podemos formalizar, exigindo que uma sequência seja aleatória, com probabilidade 1. Procuramos então, definições de “não aleatoriedade” que selecionem…a partir de todas as sequências, uma coleção cuja probabilidade seja “zero” (‘vácuo quântico’!?…). Outra definição de aleatoriedade concebe um “processo efetivo universal”…para testar a “não aleatoriedade” de uma sequência…Por fim, uma 3ª alternativa adota uma estratégia altamente intuitiva:
“Considere-se um computador programado para gerar… – como dados de saída, a sequência de resultados experimentais que efetivamente ocorrem. Que tamanho poderia ter.. – o menor programa… – que consiga fazê-lo?”
É óbvio que há um programa que irá sempre funcionar…a instrução diz apenas – Imprimir (#.&.%), em que (#.&.%) é a sequência em questão. Contudo, as sequências ‘não aleatórias’ têm programas mais curtos. Por exemplo, a sequência Cara, Coroa, Cara, Coroa…pode ser apenas ‘Imprimir Cara e Coroa, alternativamente’. Desse modo, uma sequência será tão menos aleatória, quanto menor o programa que lhe dá origem. (Occam agradece!)
“Processo estocástico” “O caráter aleatório de um número significa por definição que não se pode produzir este número por meio de um programa mais curto que ele próprio – ou seja, não se pode extrair mais informação de um sistema – do que aquilo que nele foi colocado.”
Em teoria probabilística, o ‘padrão estocástico‘ é aquele com origem em “eventos aleatórios”, cujo estado é indeterminado. Por exemplo, o lançar de dados resulta em processo estocástico…pois qualquer uma de suas 6 faces tem igual probabilidade de ficar para cima após o arremesso. – Assim, qualquer sistema, ou processo analisado usando a teoria probabilística, ao menos em parte é estocástico. – Mas é importante salientar uma diferença entre “aleatoriedade” e “estocasticidade“… – Normalmente, “eventos estocásticos são…aleatórios” – todavia, podem eventualmente não o ser. É plausível embora improvável que – numa série de 10 arremessos de dados – surjam sequências não aleatórias, tais como 6, 5, 4, 3, 2, 1, 2, 3, 4, 5 ou 1, 1, 1, 1, 1, 1, 1, 1, 1, 1.
Apesar de coerente ou compressível (podendo ser expressa de um modo mais comprimido que a sequência inteira), a sequência não-aleatória é estocástica, pois surgiu de um evento aleatório… – o “lançar de dados”.
4) Interpretações subjetivas da ‘probabilidade‘ “O homem não é nada em si mesmo. Não passa de uma probabilidade infinita. No entanto…ele é o responsável infinito dessa probabilidade”…(Albert Camus)
Uma compreensão da natureza da probabilidade radicalmente diferente de todas as perspectivas objetivas que vimos até agora, concentra-se não no que está no mundo, mas, antes, no que está em nós. Usamos a probabilidade como um guia de ação face ao risco, apostando num dado resultado, só se acharmos que as hipóteses de ganhar são suficientemente elevadas para ultrapassar nossas dúvidas… sobre se o resultado irá efetivamente ocorrer. – Assim, concebemos a ‘probabilidade’ como uma medida do nosso grau de confiança na ocorrência desse resultado. Mas, que probabilidades deverá o ‘agente racional’ atribuir aos acontecimentos…para descrever e justificar o processo subjetivo de sua súbita alteração…à expectativa de uma nova informação?
Se, para o “objetivista”…as probabilidades são características do mundo à espera de serem descobertas, para o “subjetivista”…são graus de crença parcial, guiando suas ações num mundo incerto.
5) Teorema de Bayes (probabilidade de A ocorrer…visto que B já ocorreu) [P(A/B) … “probabilidade a posteriori” — P(A) … “probabilidade a priori”; P(B/A) verossimilhança (dados); P(B) probabilidade marginal (evidência)]
Um teorema fundamental da… “teoria das probabilidades” – o ‘Teorema de Bayes’, relaciona a probabilidade de uma hipótese com base na informação (probabilidade condicional), com a ‘probabilidade condicional da informação’…dada a observação de uma ‘evidência‘ – e a ‘probabilidade inicial’ de que a hipótese seja ‘verdadeira’.
Suponha que depois de obtida a informação achemos necessário adotar … para determinar nossa ‘nova probabilidade’ – relativa à verdade da hipótese, a sua velha probabilidade — condicionada à informação. — Para isso…então, precisamos de uma ‘maneira’ de atualizar nossas probabilidades, à luz… – dessa nova informação.
Este processo, conhecido por “condicionalização“, pode ser generalizado, de modo a abranger casos em que não se conhece, com certeza, novas informações. Dessa forma, a princípio, poder-se-ia pressupor que uma moeda…(que poderia estar viciada)…possui a probabilidade 1/2 de sair…‘cara‘. À medida que novos lançamentos forem efetuados, o agente modificará a probabilidade…pelos novos resultados observados…Ao obter novas probabilidades para certas hipóteses à…’luz da informação’ – usamos as probabilidades iniciais…no que respeita à verdade das hipóteses em causa. Entretanto, nesse caso, não teríamos por isso, de começar com uma plausibilidade ‘intrínseca‘ relativa às hipóteses: as assim chamadas “probabilidades a priori”?… — E qual poderia ser a sua origem?
Quando tentamos compreender, exatamente, de que modo deveria a probabilidade entrar na Física…as disputas entre filósofos – com respeito à natureza da probabilidade, e acerca da origem e justificação das atribuições de probabilidades iniciais são cruciais. Outrossim, várias descobertas físicas… – não só esclarecem “problemas filosóficos”… – como revelam “questões adicionais”… – que complicam ainda mais a situação desses problemas teóricos.
 Alguns especialistas defendem, que só devíamos aceitar hipóteses probabilísticas em nosso corpo técnico – com base em ‘frequências observadas’, encaradas como “informação“… Alega-se, que podemos gerar “probabilidades intrínsecas“ às hipóteses – sem nos firmarmos a frequências observadas… Na verdade, essas “probabilidades a priori”, foram objeto dos trabalhos teóricos, já há bastante tempo — durante os séculos 17 e 18.
Alguns especialistas defendem, que só devíamos aceitar hipóteses probabilísticas em nosso corpo técnico – com base em ‘frequências observadas’, encaradas como “informação“… Alega-se, que podemos gerar “probabilidades intrínsecas“ às hipóteses – sem nos firmarmos a frequências observadas… Na verdade, essas “probabilidades a priori”, foram objeto dos trabalhos teóricos, já há bastante tempo — durante os séculos 17 e 18.
Se lançarmos uma moeda, há 2 resultados ‘simétricos‘ possíveis: cara e coroa. Mas, então, não parecerá razoável presumir inicialmente que a probabilidade de cada uma delas é 1/2?… Se lançarmos um dado, há 6 faces simétricas…Não devemos, então, na falta de indícios a favor da ideia de que os dados estejam viciados… — atribuir 1/6 de probabilidade… – a cada resultado com uma face específica fica voltada para cima?…
Chegaríamos assim, pelo…“Princípio da Indiferença” – a probabilidades a priori, dividindo os resultados em casos simétricos… e, atribuindo a cada um a mesma probabilidade.
Se quisermos escolher uma linguagem para descrever o mundo, podemos encontrar vários meios de ordená-lo em “possibilidades simétricas“… A probabilidade inicial é então…distribuída sobre as possibilidades de modo intuitivo e simétrico. – Uma vez obtidas as nossas probabilidades “racionais” a priori… podemos modificá-las face à informação experimental (em especial, face à informação sobre frequências efetivas observadas de resultados)… utilizando o “processo de condicionalização” já descrito.
6) As 4 “causas” de Aristóteles “Não desejamos apenas descrever o mundo que vemos, mas também — explicar a razão do que nele acontece”.

A noção intuitiva de ‘causa‘ tem desempenhado um papel fundamental na tentativa de analisar a noção de explicação científica desde que ocorreu pela 1ª vez a um filósofo tal problema… Explicar um acontecimento é indicar sua causa…Explicar uma ‘classe’ de acontecimentos…é indicar o tipo de causa que os produz… – Numa das primeiras análises da causalidade, Aristóteles distinguiu 4 tipos diferentes de causas…a matéria em que a mudança ocorre…a natureza da mudança; o fim, ou propósito da mudança; e o seu…“responsável imediato“. — A estas causas… as designou: materiais, formais, finais, e eficientes.
A questão dos fins, ou propósitos (causas finais), ainda suscita muita discussão. Talvez na ‘biologia‘…(explicações funcionais de um órgão, por exemplo)…e também nas ciências sociais, algo parecido com a ideia aristotélica…segundo a qual, indicar uma finalidade, ou propósito causal… represente algum “poder explicativo”… – possa ainda parecer atraente. Mesmo na física, não é certo que, absolutamente, não exista algum lugar para as “causas finais“. Alega-se por vezes que a explicação do percurso da luz, em termos de que demore o menor tempo possível…tem ‘natureza finalista‘. Também na ‘termodinâmica‘ tem-se defendido que explicar um processo pela “concepção do avanço” do sistema a um “estado de equilíbrio” (como um objetivo a ser alcançado)…significa usar a noção de “causa final”.
Porém, quando o “cientista contemporâneo” pensa em causas…pensa habitualmente em causas eficientes…ou seja…nos acontecimentos que irão originar a ocorrência…de um acontecimento a ser explicado. Mas, o que é explicar um acontecimento demonstrando a sua ‘causa eficiente’?…A ideia intuitiva parece ser a de que, se explica um acontecimento quando se descobre um evento anterior … que torne necessária a ocorrência desse outro. Ligar um interruptor causa acender a…‘luz‘; empurrar um objeto causa sua “aceleração”, e assim por diante… – Mas, qual seria a natureza desta transação…que torna apropriado descrever a ‘causa’ como algo que produz o…’efeito’ – ou, o…”acontecimento explicado”?
Num exame crítico merecidamente famoso sobre a noção de causalidade…David Hume defendeu que…seria errado conceber as relações causais como algo que se baseasse num “nexo causal”, ou “conexão necessária especial” entre acontecimentos…Hume defendeu que… o que encontramos no mundo quando olhamos para acontecimentos relacionados causalmente é… antes de tudo, uma relação espaçotemporal entre esses acontecimentos, pela qual o ‘acontecimento da causa’…precede no tempo…o ‘acontecimento do efeito’. Também descobriu, que – acontecimentos constantemente conjugados – estão contidos numa classe de pares de acontecimentos do mesmo tipo. Isto é, o acontecimento 1 causa o acontecimento 2 – somente se: 1 e 2 têm a relação espaçotemporal apropriada – e…se, aos acontecimentos do tipo 1…se seguem sempre acontecimentos do tipo 2; e vice-versa.

Segundo Hume…embora pensemos explicar esta conjunção constante de tipos de acontecimentos, ao dizer que os acontecimentos do tipo 1 causam os do tipo 2, na verdade, ao falar de causalidade, só reescrevemos essa ‘conjunção constante‘ – ao supormos que… – o acontecimento da ‘causa‘ torna necessário o acontecimento do…‘efeito‘.
Hume entendeu, que ‘necessidade’ não é reflexo de uma relação real entre acontecimentos, mas sim, a projeção nele de um ‘fenômeno psicológico‘. Ao vermos que acontecimentos do ‘tipo 1‘ são sempre seguidos por eventos do ‘tipo 2‘…nos acostumamos tanto à ‘sequência de fenômenos‘, que…quando temos a experiência de um acontecimento do 1º tipo…nascer do sol, por exemplo, nossa mente imediatamente ‘salta’…para a ‘expectativa’ da ocorrer um evento do tipo 2 (crepúsculo), e daí deduzimos uma (fictícia) ‘relação causal‘. Fundada no “hábito”…tal expectativa explica o motivo do 1º tipo de eventos tornar necessário o 2º.
No entanto, para Hume, isto é uma “questão psicológica“. Tudo o que há no mundo dos próprios acontecimentos são relações espaçotemporais de ‘continuidade’ e ‘precedência’, e a conjunção constante de eventos dos tipos em questão. Por outro lado defende-se que, se tais “fatos explicativos” não tiverem o tipo correto de “relação causal” com o evento explicado, conexões entre suas descrições, mesmo satisfeitas as condições desse ‘modelo dedutivo‘…não se tornarão explicações. — Por exemplo…podemos derivar a posição que um planeta ocupava ontem – a partir das leis da dinâmica, e da sua posição e velocidade de hoje; mas isso não explica por que razão o planeta estava ontem nessa posição – pois é o passado quem explica o futuro — “a direção da causalidade vai do passado ao futuro”.
“Explicar é revelar causas!“… – Entretanto…2 acontecimentos dados podem estar correlacionados de uma maneira formal… – por serem o efeito comum de um terceiro acontecimento que seja a sua causa comum…Deste modo, os 2 acontecimentos não se explicam mutuamente – embora ambos se expliquem pela mesma causa… Mas, então qual será o elemento causal (adicional) necessário para a explicação desta conjunção?
7) Explicações por ‘probabilidades estatísticas‘
 Muitos especialistas que pensam no “modelo dedutivo” como, por demais exigente; referem-se às “explicações históricas”… Aí, as respostas parecem ser aceitas…sem quaisquer generalizações formais… — Mas, nesse caso, quais seriam as…”leis dos acontecimentos históricos”? Parece evidente que, nestas explicações…os eventos se conectam por meio de ‘generalizações‘…pelas quais, estas não são leis da natureza ‘irrefutáveis‘ – mas sim, “conexões probabilísticas“… – entre estes eventos.
Muitos especialistas que pensam no “modelo dedutivo” como, por demais exigente; referem-se às “explicações históricas”… Aí, as respostas parecem ser aceitas…sem quaisquer generalizações formais… — Mas, nesse caso, quais seriam as…”leis dos acontecimentos históricos”? Parece evidente que, nestas explicações…os eventos se conectam por meio de ‘generalizações‘…pelas quais, estas não são leis da natureza ‘irrefutáveis‘ – mas sim, “conexões probabilísticas“… – entre estes eventos.
Fumar nem sempre causa câncer do pulmão, mas certamente aumenta sua probabilidade. Não teremos então, oferecido pelo menos uma explicação parcial para o fato da pessoa ter um câncer de pulmão se indicarmos que essa pessoa fuma muito – mesmo que fumar não produza, necessariamente, tal doença?… – Que tipo de “relação probabilística” … entre os eventos explicativo e explicado…será suficiente, para se dizer que um demonstra o outro?
Um pensamento que naturalmente logo ocorre, é o de que um acontecimento se explica, ao encontrarmos outros eventos…tais que sua ocorrência se siga de fenômenos com alta probabilidade. Constatamos assim que tal “explicação estatística“ dos acontecimentos é bem diferente de uma explicação em que se usem “leis naturais”…No caso dedutivo, por exemplo…ao explicarmos os acontecimento 1, e o 2…podemos produzir uma explicação automática … conjugando apenas recursos explicativos usados para cada acontecimento individual… — “o acontecimento 1…ocorreu – e o acontecimento 2…ocorreu”. Mas…se o acontecimento 1 se segue de uma base explicativa com elevada probabilidade; e, se o acontecimento 2 se segue da sua base explicativa…com probabilidade igualmente alta…não há garantia que os acontecimentos 1 e 2 se sigam conjuntamente…pelas bases explicativas conjugadas – com uma probabilidade acima do valor mínimo. – Além disso, se por acaso, um acontecimento possuir uma probabilidade elevada relativamente à sua base explicativa…poderá ter essa probabilidade reduzida – ao incluir…mais informação.
Podemos então, explicar um “acontecimento” … através de fatos aos quais ele tem uma probabilidade relativamente reduzida, fazendo notar que… sem estes fatos explicativos, o ‘evento’ em questão teria uma probabilidade ainda mais reduzida…Explicamos assim, por que razão acontece algo, nos referindo a fatos que tornam esse acontecimento mais provável, mesmo que depois da adição destes fatos… sua probabilidade continue baixa. Constata-se também, casos em que explicamos um evento por outro…mesmo que, com a nova informação…sua probabilidade em relação ao conhecimento de fundo se reduza.
A ideia aqui em jogo, é a de que um acontecimento pode causar diversas consequências, tendo cada uma delas…uma probabilidade específica de ser a ‘causadora’. Embora uma causa possa resultar numa multiplicidade de efeitos – é ainda uma “relação causal” que produz…o “acontecimento do efeito“… – a partir do “acontecimento de origem“.
8) Relações Causais, e Determinismo Ao sermos capazes de distinguir as correlações…que, por não serem causais, não são explicativas, das correlações explicativas, que…mesmo que sejam probabilísticas, são genuinamente causais, surgem daí novas questões interessantes. Será que ao darmos uma explicação probabilística causal – somos forçados a defender que no mundo…há relações causais irredutivelmente probabilísticas?…Será que precisamos afirmar que, na sua base…“o mundo tem natureza genuinamente aleatória”, não sendo regido por “relações causais” inteiramente “determinísticas”?… – “Não… necessariamente”.
Há quem defenda a possibilidade de…”justificações probabilísticas” que expliquem um ‘evento’ como resultado “puramente aleatório”, de certos fatos antecedentes…os quais tenham…“formas causais” para gerar resultados desse tipo.
Noutros casos – a probabilidade pode ser explicada…graças à sua “relação causal” se fundamentar em certas “relações subjacentes” completamente “deterministas“.
Neste 2º tipo de explicação, o ‘estado posterior’ de um sistema será inteiramente determinado – pelo seu “estado dinâmico inicial“.
Muito embora vários estados dinâmicos iniciais possíveis se tornem consistentes com a descrição inicial do sistema…com cada um desses ‘estados iniciais‘ tendo um resultado futuro diferente…”cada evolução é inteiramente determinista“. Dessa forma…a probabilidade entra na explicação, quando começamos a falar da “probabilidade de um certo estado dinâmico inicial” – “consistente com a descrição inicial do sistema“.
Temos então ‘elementos probabilísticos’ na nossa estrutura explicativa, numa base que consiste em ‘processos causais subjacentes’, geradores de fatos a se explicar…Daí, como consequência, a probabilidade surgirá; não por uma…“relação causal, intrinsecamente aleatória” – mas pela exploração de muitas, das diferentes ‘evoluções causais‘ possíveis.
Por essa perspectiva, a tese de se postular uma “causalidade genuinamente aleatória” ao tratarmos da ‘mecânica quântica‘, passa a ter algum sentido.
Ao tentarmos explicar um evento em termos probabilísticos, procuramos colocá-lo em uma estrutura de ‘relações causais’ – de forma probabilística…ou por ‘relações causais’ intrinsecamente indetermináveis – ou, ao se considerar – simultaneamente – diversas evoluções causais alternativas, relacionando-se entre si. – Mas, até com probabilidade reduzida em sua cadeia causal … pode-se explicar um fato. – Será então, que toda esta importância à revelação de ‘relações causais’ em explicações significaria desprezarmos nossa teoria humana, sobre uma coisa ser a causa de outra?… – Não, necessariamente.
Há quem defenda que…como as explicações exigem referência às relações causais entre acontecimentos – devemos pressupor a noção de “relação causal” como um elemento primitivo na nossa compreensão da natureza do mundo. – Até mesmo, sublinha-se com frequência…que a estrutura do mundo só nos faz identificar uma “conjunção constante” como uma “relação causal” … se os eventos em questão estiverem ligados por percursos apropriadamente contínuos de acontecimentos constantemente conjugados … havendo assim, a necessidade dessa ‘influência‘, ou “propagação causal”, na base epistemológica.
9) ‘Funções de causalidade’, “leis formais“, e “correlações probabilísticas“ “Biologia, química e física, por exemplo, são usadas para complementar a correlação manifesta, com correlações mais sutis…presentes nas leis mais profundas da ciência”.
É muito importante refletir sobre o fato das regularidades inteiramente formais…ou meramente probabilísticas, que usamos nas explicações científicas – formarem uma ‘hierarquia unificada de proposições’… – dentro de uma ‘estrutura teórica-científica’. De fato, algumas dessas generalizações são mais amplas, profundas, e fundamentais que outras, podendo-se argumentar, inclusive, que…o que faz as correlações causais apropriadas às explicações — se justifica pelo fato delas integrarem a correlação dos acontecimentos… – em seus níveis mais profundos… das teorias mais fundamentais. Nessa perspectiva, a exigência de ‘causalidade‘ nas explicações está garantida… ‘não por fundamentos humanos, mas sim através de princípios tecnicamente imparciais’.
Este aspecto da função da causalidade em explicações é especialmente relevante aos nossos propósitos… – À proporção que se vislumbra o papel da probabilidade na ‘mecânica estatística‘ observamos que a termodinâmica – uma teoria de nível superficial do comportamento macro… se relaciona, em “termos explicativos”…com uma teoria dinâmica de “nível profundo”.
Esta teoria de nível profundo, é a teoria do comportamento de sistemas…fundada nas leis básicas da dinâmica dos componentes microscópicos…a sistemas macroscópicos (…tal como as moléculas de um gás).
As considerações probabilísticas surgem quando tentamos integrar os 2 níveis descritivos, usando a teoria de nível profundo, para explicar a ‘teoria emergente’. Assim, pressupõe-se que podemos apresentar uma explicação causal da evolução do sistema pela dinâmica dos seus constituintes microscópicos, numa descrição científica ampla e fundamental… Nesse sentido, nossa discussão tem avançado…como se os acontecimentos específicos fossem os objetos primários da compreensão científica. – Contudo, cientificamente…generalizações formais…como leis, ou ‘correlações probabilísticas‘…são abordagens mais utilizadas.
A ideia principal é que… – sendo “abstrações formais”, estatísticas inteiramente legítimas, podem elas ser explicadas quando focadas sob generalizações… mais amplas… profundas… e… fundamentais.
As leis formam uma ‘hierarquia’…que vai de generalizações superficiais limitadas, como a lei da refração de Snell… na ótica, ou lei de Ohm/eletricidade (leis de ordem inferior); às leis mais gerais e profundas… das teorias físicas fundamentais (leis de ordem superior).
As ‘leis de ordem inferior’ podem aplicar-se só em certas circunstâncias específicas, que podem ser bem definidas…em condições específicas apropriadas. – Explicamos a “ótica geométrica” ao mostrar que ela se segue da “ótica física” (ondulatória); sendo esta, uma consequência da “teoria eletromagnética”. – Já o “eletromagnetismo” é explicado como um componente do “campo eletrofraco”, descrito pela “teoria quântica dos campos”…e, assim por diante… – Geralmente, a ideia é que se explicam as leis mais superficiais…ao derivá-las – a partir de leis de um tipo mais geral…e fundamental. Mas…na verdade, as coisas são muito mais complicadas. Afirma-se com frequência que ao se explicar as leis mais superficiais, se descobre que normalmente não são verdadeiras. Em muitos casos são apenas boas aproximações à verdade, e mesmo assim…só em certas circunstâncias.
Quando leis e generalizações estatísticas mais superficiais…que se pretende explicar, apresentam conceitos diferentes dos usados nos ‘princípios explicativos’ mais profundos, surgem questões bem problemáticas… – Isto ocorre sempre que uma teoria menos profunda for reduzida a uma mais profunda…exigindo que se faça uma conexão entre os conceitos das 2 teorias – que…por vezes são bastante diferentes…Enquanto, por exemplo…a biologia fala de organismos e células, a química molecular fala de coisas como moléculas, ou graus de concentração.
10) A dualidade termodinâmica “Ao nível explicativo mais fundamental, situam-se as leis dinâmicas dos constituintes microscópicos”.
Como estarão as células relacionadas com seus constituintes microscópicos? Essa resposta parece evidente… já que células são feitas de moléculas…mas é fato que apesar de lidar com ‘aspectos macroscópicas do mundo‘…tais como temperatura – quantidade de calor…e entropia — a ‘termodinâmica’ trata sistemas… — a partir de constituintes microscópicos… — como “moléculas”.
Embora objetos macroscópicos sejam feitos de ‘componentes microscópicos’, é tarefa bem complexa relacionar as propriedades dos sistemas — tais como entropia, calor e temperatura) ao nível que se pretende explicar — em nº de constituintes microscópicos e espaço a que estão limitados … assim como às suas próprias “micro-características” (‘quantidade de movimento’ – energia, massa, dimensão). E isto é ainda mais difícil pela interação que ocorre nesta ciência, entre as leis que não admitem exceções e generalizações estatísticas.
Estas leis não admitem exceções…embora na versão probabilística, que faz da “mecânica quântica“… uma “teoria fundamental“, contenham em seu escopo um elemento intrinsecamente estatístico.
Mas, é bom notar que, entre as leis dinâmicas fundamentais dos microconstituintes, e as leis da teoria a ser reduzida, existem ‘generalizações‘, introduzindo elementos estatísticos, ou probabilísticos, na imagem explicativa. Por isso…defende-se que a dinâmica fundamental explica o ‘comportamento térmico‘…ao nível macroscópico, como o comportamento ‘absurdamente‘ mais provável…ou, noutros casos… como o ‘comportamento médio previsto’.
Quando tentamos compreender a mecânica estatística, as questões mais interessantes e importantes surgem, exatamente neste ponto.
Como as “generalizações estatísticas” – que formam os postulados centrais da teoria…se relacionam…por um lado… com a ‘dinâmica das leis fundamentais’ dos micro-elementos do sistema… – e… por outro, com as ‘leis do comportamento macroscópico’, controladas pelos conceitos da física térmica tradicional.
Por conseguinte, a explicação comportamental do sistema ao nível macroscópico, deve ser apresentada em termos correspondentes à uma consequência do sistema menor, formado por partes microscópicas…em termos das leis fundamentais que regem a dinâmica dessas partes, e por meio de um esquema explicativo, que introduza a nível intermediário noções fundamentalmente probabilísticas e estatísticas. – Mas, o que fundamentará a introdução destes postulados, e pressupostos probabilísticos adicionais?… – Poder-se-á derivá-los da própria dinâmica fundamental, ou sua introdução na física demandará novos postulados?
Esta é uma questão em aberto… difícil e complexa, mas muito importante, pois sua resposta definirá … o nível de explicação que a ciência física pode oferecer a fenômenos macroscópicos.
Lawrence Sklar…“Probabilidade e explicação estatística, segundo os filósofos” Universidade de Michigan (‘Philosophy of Physics’, Oxford University Press…1992). *****************************************************************************
Causalidade & Probabilidade Enquanto a ‘ideia de triângulo‘ não se alterar… — a soma de seus ângulos internos corresponderá a 2 ângulos retos, e essa igualdade sempre se verificará. (David Hume)
O filósofo David Hume distingue conhecimento e probabilidade, da seguinte forma: No conhecimento, as “relações de ideias”…dependem das próprias…’ideias‘…Então, para que essa relação se altere, é preciso que também se troque essa ideia. Por outro lado, há o que Hume chama “probabilidade”…cujo conceito trata de relações de fato, não das relações racionais… – Ao contrário do conhecimento… onde negar a relação implica em uma ‘contradição’, na probabilidade negar a relação é uma possibilidade.
Para Hume existem 3 relações na probabilidade: a ‘identidade‘…’situações‘ (tempo e lugar)…e, ‘causalidade‘. Sobre esta, Hume diz ser um raciocínio baseado em conexões de causa e efeito, constatados na experiência. Para Hume, quando dizemos que o fato A causou B – não havendo experiência que sustente a relação – trata-se de um ‘raciocínio arbitrário‘. — Assim…Hume critica os que recorrem à razão para esclarecer a origem da ideia de causalidade — e creem que relações de causas e efeitos possam se constituir em objetos de “genuíno conhecimento”. Para o filósofo…o raciocínio de causa e efeito é, em síntese, um ‘raciocínio provável’ cujo fundamento só é dado na experiência. (texto base) **********************************************************************************

“Expectativa” (“Teoria dos Jogos”)
Expectativa, filosoficamente falando, é o ‘grau de justiça’ de um determinado jogo.
Jogos de azar envolvendo probabilidades são muito populares… em todo o mundo, vamos então ver algumas noções básicas:
Considerando que um “jogo de roleta” tenha n possíveis resultados: A1, A2, A3…An; e cada um desses resultados, com probabilidades P1, P2, P3…Pn, onde P1+P2+P3+…Pn=1… e ainda, supondo que o prêmio para cada jogada Ai é Vi… Então, chamamos de ‘expectativa‘ ao ‘valor esperado’…E=(V1.P1)+(V2.P2)+(V3.P3)+…(Vn.Pn) que um jogador “espera” ganhar (em média) a cada jogada. – Se por acaso E for ‘positivo’, o jogo é favorável ao jogador; caso contrário…é desfavorável. Mas, se E=0, o jogo é justo.
Em um jogo de 2 dados – por exemplo…se a soma der 7 ou 11…e o jogador ganhar R$7,00; ou – caso contrário, perder R$2,00… podemos calcular a expectativa da seguinte forma: a probabilidade vitoriosa é calculada determinando quantas maneiras possíveis de se chegar à soma 7 ou 11…são elas: (1 e 6) (2 e 5) (3 e 4) (4 e 3) (5 e 2) (6 e 1) e (5 e 6) (6 e 5); ou seja, 8 maneiras…em um total de (6×6=36) possibilidades. — Desse modo… a probabilidade do jogador ganhar é 8/36 = 2/9… enquanto a probabilidade dele perder é (36 – 8)/36 = 28/36 = 7/9. – Nessas condições, então…a expectativa é (2/9.R$7,00) – (7/9.R$2,00) = 14/9 – 14/9 = 0; e…portanto – o jogo é justo. (Michel Janos – “Matemática e Natureza”) ************************************************************************************
A teoria dos Jogos (e a mente brilhante de John Nash)
Tratamos aqui da Teoria dos Jogos pelo estudo do equilíbrio de estratégias dominantes, e do equilíbrio de John Nash em jogos não cooperativos. — Discorremos uma narrativa histórica do seu desenvolvimento, apresentando conceitos envolvidos e suas aplicações.
 As crianças costumam brincar — pelo o simples prazer de divertir-se…com jogos que podem ser de tabuleiro…esportivos, de recreação, jogos de azar — ou… até mesmo … mais modernamente, jogos eletrônicos (videogames). Em todos esses jogos — o objetivo de cada jogador é vencer… e, na maioria das vezes… — derrotar o adversário.
As crianças costumam brincar — pelo o simples prazer de divertir-se…com jogos que podem ser de tabuleiro…esportivos, de recreação, jogos de azar — ou… até mesmo … mais modernamente, jogos eletrônicos (videogames). Em todos esses jogos — o objetivo de cada jogador é vencer… e, na maioria das vezes… — derrotar o adversário.
Na vida adulta, em algumas situações, esses jogos podem deixar de ter o caráter de divertimento…e, então…assumir contornos mais sérios e objetivos.
Nessa linha…podemos imaginar um candidato a uma vaga de emprego que precisa disputar com outros concorrentes diversas etapas de um ‘processo de seleção’…Ou ainda uma empresa que precisa disputar com outras uma concorrência; para obter um contrato de prestação de serviços – ou, para fornecimento de mercadorias. Em Economia há um pressuposto clássico, de que pessoas e empresas agem de “forma racional“ – isto é, tomam decisões que provém de uma análise criteriosa de custos e benefícios … e, primordialmente — buscam o objetivo que julgam melhor para si. Nesse caso então, concluímos que – tanto pessoas como empresas buscam sempre obter vantagem em jogos que disputam; por um pouco mais de satisfação ou lucro.
Entender as estratégias dos jogadores e quantificar as vantagens envolvidas em um jogo é o objetivo da “Teoria dos Jogos” – visando a racionalidade das decisões tomadas pelos jogadores…na busca da melhor estratégia – ou seja, daquela que dará a maior vantagem, seja na forma de mais lucro…ou maior satisfação. – E…para isso…muitas delas têm sido estudadas usando o aparato da… “Teoria dos Jogos” — que se ocupa da análise geral das estratégias de interação — como…jogos de azar, negociações políticas, e comportamento econômico – sendo uma metodologia vital para muitas disciplinas…incluindo economia, ciência política, biologia e direito…portanto, um campo de estudo de muita importância.
A Teoria dos Jogos é particularmente importante para o estudo dos oligopólios em Microeconomia. Um ‘mercado oligopolista’ é aquele em que há poucos vendedores oferecendo produtos similares. Como resultado, as ações de qualquer vendedor do mercado podem ter grande impacto sobre os lucros de todos os outros…ou seja, as empresas oligopolistas, ao possuírem controle de parcela significativa da demanda, são…”interdependentes”…de uma forma que as “empresas competitivas”…não são.
Origens históricas A lógica comportamental humana tem sido provada há milênios…Em tempos antigos, vários códigos civis e religiosos estabeleceram padrões de negociação, contratos e punições… de uma forma semelhante – ao que é feito hoje em dia.
 Por exemplo…o “Talmude Babilônico” já estabelecia regras para a divisão de bens, que podiam prenunciar teorias atuais da repartição de herança… — o que poderia impactar na relações de interesse… Com efeito, há centenas de anos matemáticos otimizavam estratégias em jogos de azar.
Por exemplo…o “Talmude Babilônico” já estabelecia regras para a divisão de bens, que podiam prenunciar teorias atuais da repartição de herança… — o que poderia impactar na relações de interesse… Com efeito, há centenas de anos matemáticos otimizavam estratégias em jogos de azar.
Esses estudos, datados dos séculos 16 e 17 deram origem à teoria das probabilidades, que modernamente costuma ser aplicada largamente em uma…“análise de decisões“. Abaixo transcrevemos o resumo de uma cronologia histórica da…”Teoria dos Jogos”:
Em 1713, Francis Waldegrave desenvolveu a primeira “solução minimax” para um jogo de 2 pessoas. A solução de Waldegrave era gerada por uma ‘estratégia de equilíbrio‘, todavia, ele trabalhou com um jogo específico, não generalizando os resultados. Augustin Cournot publicou, em 1838, um trabalho no qual, utiliza uma solução conceitual…que se configura como uma versão restrita do que mais tarde ficou conhecido como “equilíbrio de Cournot-Nash”…Em 1871, Charles Darwin formulou implicitamente o primeiro argumento teórico sobre a “Teoria dos Jogos” em seu trabalho sobre “evolução das espécies”…Ernst Zermelo publicou, em 1913, o primeiro teorema da ‘Teoria dos Jogos‘, resultado de uma análise do “jogo de xadrez“. – Denes Konig e Laszlo Kalmar prosseguiram no trabalho e publicaram então artigos aprofundando o assunto. – Em 1921, Emile Borel publicou alguns trabalhos inovadores sobre jogos de estratégias — criando a primeira formulação de uma estratégia mista – utilizando ‘probabilidade’ para encontrar uma solução para um jogo de 2 pessoas.
Foi então que, entre a década de 1920 e 1940, John von Neumann propôs uma rigorosa teoria de situações estratégicas…e junto a Oskar Morgenstern, publicou o 1º livro sobre ‘Teoria dos Jogos’. Eles mostraram detalhadamente como representar os jogos em uma forma matematicamente precisa, por um método de análise comportamental. Contudo, foi John Nash quem impulsionou o avanço da teoria, mostrando a distinção entre jogos cooperativos e não cooperativos, dando a ambos o conceito de comportamento racional.
“O dilema do prisioneiro” Exemplo fundamental da Teoria dos Jogos, estudado pela 1ª vez no início da década de 1950…que caracteriza toda uma classe de problemas semelhantes.
Dois ladrões são presos portanto armas, mas nenhuma evidência é encontrada que possa liga-los a outros crimes. – A polícia leva-os para salas separadas … e faz uma proposta a cada um deles … caso confesse seus crimes e seu parceiro não – ele será libertado e o outro ladrão será condenado a 10 anos de prisão. Porém, recusando a cooperar…e o parceiro confessando – ele é quem será condenado a 10 anos – e seu parceiro libertado. – Se ambos confessarem, serão sentenciados a 5 anos de prisão, mas se ambos não cooperarem, a polícia…sem mais provas…só os condenará por 6 meses pelo porte de armas…A polícia informa a cada um deles que a mesma oferta é feita a ambos; mas como não podem se comunicar entre si, são obrigados a jogar com suas estratégias disponíveis, mostradas no quadro 1, chamado “matriz payoff”.

Quadro 1: o dilema do prisioneiro (matriz de resultados)
É notório que avaliando vantagens e desvantagens, seria bom para ambos se eles não confessassem nada. Entretanto cada prisioneiro deve analisar o que é melhor para si, considerando que não se sabe a decisão do outro. Assim, vamos pensar na estratégia do Ladrão A – se o ladrão B confessar…a melhor decisão a tomar é confessar – se o ladrão B não confessar, a melhor decisão para ele é confessar. Dessa maneira, vemos que, independentemente da decisão do ladrão B, a melhor estratégia para o ladrão A é confessar. Isto também vale sob a ótica do ladrão B. – Podemos então concluir que, sendo a decisão racional tomada por ambos…eles são condenados a 5 anos de prisão.
O dilema do prisioneiro é um jogo não cooperativo…e como a estratégia dominante para ambos os jogadores é a mesma…a solução do jogo é chamada de ‘equilíbrio de estratégia estritamente dominante’. Esse tipo de resultado também é chamado de ótimo de Pareto, na medida em que a estratégia definida para ambos não é dominada por outra qualquer. Mas, na maioria dos jogos inexiste um equilíbrio de estratégia ‘estritamente dominante’; a melhor estratégia para um jogador é diferente daquela do outro jogador. Nesse caso, a forma mais genérica de equilíbrio, com várias estratégias, chama-se ‘equilíbrio de Nash‘.
Estratégias dominantes: Eu estou fazendo o melhor que posso, independente do que você esteja fazendo…Você está fazendo o melhor que pode… – independente – do que eu esteja fazendo.
Equilíbrio de Nash: “Eu estou fazendo o melhor que posso, em função daquilo que você está fazendo. — E você está fazendo o melhor que pode… – em função daquilo que eu estou fazendo”.
“O jogo da propaganda” Para ilustrarmos a ideia de ‘equilíbrio de Nash’ reproduzimos um jogo no qual duas empresas vendem produtos concorrentes – e estão decidindo se farão ou não propaganda dos seus novos produtos. O quadro abaixo mostra sua matriz de resultados — admitindo-se uma simultaneidade na… “tomada da decisão“.
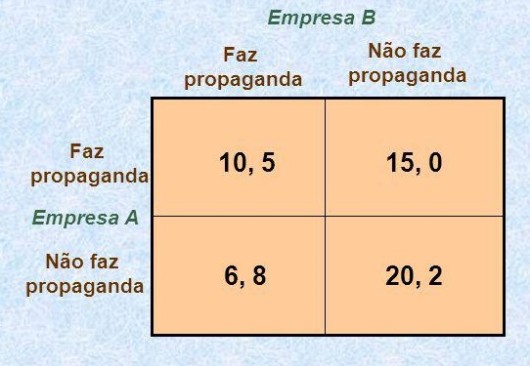
Quadro 2: o jogo da propaganda
Vemos aqui que a empresa A não tem ‘estratégia dominante‘. Se a empresa B decidir fazer propaganda – a melhor estratégia da empresa A é também fazer propaganda. Porém, se a empresa B decidir ‘não fazer’ propaganda, a melhor estratégia para a empresa A é não fazer propaganda. Assim, a estratégia a ser definida pela… empresa A — é acompanhar a mesma decisão da… empresa B.
Vejamos agora o jogo pelo lado da empresa B. Se A decidir fazer propaganda, a melhor estratégia para B é não fazer propaganda. E, se A decidir ‘não fazer’ propaganda…a melhor estratégia para B segue sendo ‘não fazer’ propaganda. A empresa B, portanto, tem uma…“estratégia dominante” – que é “não fazer propaganda”…independente da decisão que a empresa A tomar. Deste modo, voltando para o lado da empresa A…se ela age racionalmente, sabendo que a decisão da empresa B é não fazer propaganda, sua melhor decisão é também não fazer propaganda. — Vemos assim, que a estratégia com a qual ambas as empresas não fazem propaganda configura-se como um “equilíbrio de Nash”.
A literatura mostra que existem diversos outros tipos de equilíbrio, assim como existem diversos tipos de jogos com características diferentes. Porém, o equilíbrio de estratégias dominantes e o ‘equilíbrio de Nash’, são suficientes para se estudar uma ampla gama de jogos econômicos. (texto base) “Prometeica” — Revista de Filosofía y Ciencias — (2015) *******************************(texto complementar)******************************
Riemann… e a Hipótese dos ‘Números primos’ “Inegavelmente a matemática é a única ‘linguagem universal’… – Podemos imaginar diferentes químicas ou biologias do outro lado do universo, mas os ‘números primos’ continuarão sendo primos … em qualquer galáxia que encontremos”. (Alain Connes)
Números primos, são aqueles apenas divisíveis por si próprios e pela unidade. Nenhum nº par…(“exceto 2″)…pode ser primo, porque todos os pares podem ser divididos por 2. – Mas, por exemplo, 3 é primo…assim como 19 também, porque não se pode dividi-los… — por qualquer outro número…além deles mesmos…e 1.
Já se sabe que os ‘números primos’ são infinitos e que existem alguns métodos para tentar localizá-los… – mas… além disso… há outros mistérios fascinantes.
Não existe até hoje alguma fórmula capaz de agrupar todos os números primos. Ainda é impossível prever…quando o próximo vai aparecer… – às vezes eles estão separados por mais de mil números…e outras vezes – por um número apenas – e esses são conhecidos como ‘números primos gêmeos‘. Mas sabemos que a distribuição dos primos, apesar de parecer aleatória, não o é… – o que acontece é que ainda não conseguimos ver qualquer harmonia nela. (E isso é muito misterioso!…) É incrível que ainda seja impossível de se encontrar um padrão para a localização deles, ainda mais se pararmos para pensar que esses números são os ‘blocos de construção‘ para qualquer outro número… – já que todo e qualquer número pode ser gerado a partir da multiplicação dos números primos.
A Hipótese de Riemann
Em 1859, o matemático Bernard Riemann fez uma ‘hipótese’ — que continua sendo o principal avanço em direção a uma ordem no caótico mundo dos… ‘números primos’. Basicamente… a ‘hipótese de Riemann’ diz que existe uma fórmula na ‘função zeta’ de Riemann…definida num gráfico 4D – com base nos números naturais, e imaginários, onde todos zeros “não-triviais” (formados por nºs naturais positivos), se agrupariam sempre, sobre a mesma linha … conectada com a localização dos… “números primos”.
O problema é que até agora ninguém conseguiu provar a hipótese de Riemann, principalmente porque os zeros, assim como os números primos, são infinitos; e, temos que achar cada zero, um por um…Até agora já foram encontrados 6,3 bilhões de zeros sobre a linha, e nenhum fora dela. Mesmo assim, ainda não é possível garantir que a hipótese seja verdadeira… – Sem um modo de prever a localização de todos os zeros é impossível provar que estejam na mesma linha.
A harmonia por trás do distribuição dos números primos continua sendo… — um dos maiores ‘mistérios’ do mundo.
Mas, talvez a prova da “hipótese de Riemann” seja tão intrincada…que o cérebro humano não consiga alcançá-la. E assim, a lógica por trás dos números primos estaria mesmo fora do nosso alcance, comprovando então o ‘teorema da incompletude‘ de Gödel, que diz que existem certas teorias, que mesmo verdadeiras, jamais poderão ser provadas. Essa é uma perspectiva triste. Mas talvez a beleza desses números, venha justamente da sua natureza egoísta, em que cada um existe totalmente sozinho – sem divisor, e sem previsão de onde estará o próximo – que pudesse compor uma paisagem maior que si próprio. (texto base) ***********************************************************************************
“Teoria Analítica dos Números (Primos)” A invenção do Cálculo Diferencial e Integral provocou um dos maiores avanços no ‘pensamento ocidental’…O trabalho monumental de Newton e Leibniz propiciou o avanço da ciência em todas suas áreas. O matemático Leonhard Euler (1707/1783) foi um dos pioneiros a usar métodos do Cálculo à ‘Teoria (Analítica) dos Números’. Contudo, o reconhecimento de tal feito…foi para Bernard Riemann (1826/1866).
Riemann revolucionou a Análise Matemática, a Geometria e a Física Matemática. Em Teoria Analítica dos Números, bem como em outras áreas da Matemática, suas ideias ainda exercem profunda influência. Variedades Riemannianas, Equações de Cauchy– Riemann, Superfícies de Riemann, e muitos outros assuntos encontram-se entre seus trabalhos. – Mas, um fato peculiar, é que a chave para alguns dos maiores problemas contemporâneos reside em uma conjectura sua, denominada “Hipótese de Riemann”:
 Tudo começou quando Euler definiu em 1740 uma função – denotada pela letra grega ζ (“zeta”)… – A “função zeta“ de Euler, associa a todo número real maior que 1 … um outro diferente — “número real”.
Tudo começou quando Euler definiu em 1740 uma função – denotada pela letra grega ζ (“zeta”)… – A “função zeta“ de Euler, associa a todo número real maior que 1 … um outro diferente — “número real”.
É interessante notar, que ao encontrar a relação ζ (2) = π2/6… Euler observou que essa função daria informações sobre o padrão dos números primos. Nascia assim, a Teoria Analítica dos Números, ou seja, o estudo dos ‘números primos’…através do Cálculo aplicado à investigação de propriedades de algumas ‘funções complexas‘. Apesar de não se visualizar um gráfico dessas funções (com dimensão 4)…é possível, com a ajuda de um bom software… – definir as partes “real“…e “imaginária” de uma tal função.
Convém observar que existem inúmeras funções zeta e alguns matemáticos costumam dizer que Teoria dos Números é o estudo de funções zeta. Porém, qual é a relação entre os “números primos” e a “função zeta” de Euler?
 “Função Zeta” dos Números primos
“Função Zeta” dos Números primos
Euler demonstrou um impressionante teorema… afirmando que para qualquer número real maior que 1…a “função zeta” se expressa como produto infinito de fatores para qualquer ‘número primo’. Tal função…foi minuciosamente investigada por Riemann ao substituir o número real (x) por um ‘número complexo‘, forma algébrica (z = a + bi); o que tornou a “função zeta” do tipo “complexa”.
Tal função não está definida para todos números complexos. Porém, Riemann percebeu que com uma técnica da “Teoria das Funções Complexas” seria possível estendê-la para todos os ‘complexos’, exceto para o número z = 1. – Em 1859, publicou seu fundamental artigo, usando a ‘função zeta’ para checar o padrão dos “números primos”…Seu objetivo era demonstrar a Conjectura de Gauss, hoje mais conhecida como ‘Teorema do Número Primo’, provando que a quantidade de números de primos entre (1 e x)…para grandes x, é aproximadamente o próprio x, dividido pelo logaritmo natural de x, isto é…(x / ln x).
Embora Riemann não tivesse obtido sucesso…seu trabalho foi de suma importância para o desenvolvimento da “Teoria Analítica dos Números“. Vários resultados foram obtidos quando da investigação das propriedades dessa função, intimamente ligadas à distribuição de números primos, ao longo de sua sequência natural no conjunto dos ‘inteiros positivos’.
O caminho de futuros progressos investigativos ficou assim esquematizado…em uma série de conjecturas bem fundamentadas…dentre as quais, a famosa “Hipótese de Riemann”.
Em 1896, os matemáticos… J. Hadamard e De la Vallée-Poussin, demonstraram, independentemente…o “Teorema do Número Primo“…utilizando as ideias então desenvolvidas por Riemann.
Consideremos a equação ζ(s) = 0. Então, qualquer número complexo s, que resolva essa equação é denominado um “zero” da equação. Riemann observou primeiramente, que os inteiros negativos pares –2, -4 –6… são zeros da função…Depois, observou que deveriam existir infinitos zeros complexos, e então estabeleceu de forma audaciosa a conjectura de que…qualquer outro zero complexo da função zeta — possui parte real igual a ½, ou seja, tem a forma (s = ½ + b i). Portanto, todos os zeros da função zeta que não são números reais estarão na reta vertical (x = ½). Essa reta é geralmente chamada de “reta crítica“.
A primeira coisa a observar é que os zeros da reta crítica não são reais, colocam-se simetricamente em relação ao eixo real e também em relação à própria reta crítica. Essa é a célebre “hipótese de Riemann“…sem dúvida, uma questão importante, pois o arranjo dos zeros da função zeta – se traduz na distribuição dos nºs primos.
A ‘Hipótese de Riemann’ foi considerada um dos problemas do milênio, pois é o problema mais importante da Matemática ainda não resolvido… — com algumas consequências em Física quântica … e, profundas repercussões na Teoria da Informação, em especial, na questão de “segurança”. (texto base) ***********************************************************************
Física explica enigma da Matemática, a Hipótese de Riemann (nov/2021) O fato da matemática fornecer à física a linguagem certa para formular as leis da natureza está na própria lógica das coisas. Porém, a possibilidade da física fornecer a ‘chave’ para a compreensão de um genuíno mistério da matemática — ao contrário… é um fato bastante incomum e extraordinário. Mas é o que agora parece estar acontecendo pela primeira vez.

A Física precisa da Matemática para quase tudo – mas ninguém imaginava que o contrário também poderia ser verdadeiro. [Sissa]
No cerne do argumento de Riemann havia uma conjectura que ele não foi capaz de provar, sobre a localização de um nº infinito de zeros – no “plano complexo” de uma certa função, conhecida como “função de Riemann“…Esses zeros parecem se alinhar “magicamente” ao longo de uma linha vertical com uma abscissa exatamente igual a 1/2…Até agora ninguém conseguiu entender a razão de uma regularidade tão incrível. Mas Giuseppe Mussardo, da “Escola Internacional de Estudos Avançados” — Itália, e seu colega André Leclair acabam de demonstrar uma explicação extremamente elegante para tal alinhamento dos zeros, ao longo do eixo 1/2 da ‘função de Riemann‘, bem como de infinitas funções semelhantes: as chamadas…”funções de Dirichlet”. – Segundo eles, em última análise, essa distribuição se deve à surpreendente presença de um “movimento caótico” e suas “leis de probabilidade”.
Na verdade, numa espécie de reciprocidade…ou simetria no conhecimento, eles provaram a existência de um movimento browniano, oculto por trás de todas essas funções infinitas: Há pouco tempo, físicos mostraram que a função de onda, que explica partículas atômicas e subatômicas, é uma matemática que virou realidade…Agora, os matemáticos mostraram que um movimento aleatório das partículas explica a presença de um ‘padrão matemático’.
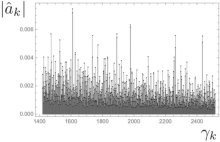
A estatística do movimento browniano explica os infinitos zeros na plotagem dos números primos. [Imagem: Giuseppe Mussardo et al.]
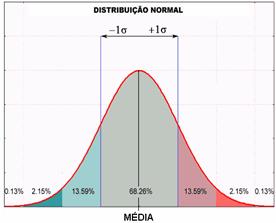
O “movimento browniano”, explicado pela 1ª vez por Einstein em 1906 – e ‘fenômeno-chave‘ na mecânica estatística, é o movimento caótico dos átomos de um gás – devido à ‘altíssima frequência’ de suas colisões. Nele, o expoente universal que rege como os átomos se espalham ao longo do tempo (1/2), se deve às leis probabilísticas de Gauss, como parte do seu famoso: “teorema do limite central“: “Quando o tamanho de uma amostra aumenta — sua ‘distribuição média‘ se aproxima de uma distribuição normal … gaussiana”.
Segundo Mussardo: “Nossa hipótese sobre a natureza browniana da conjectura de Riemann…amparada numa série de resultados probabilísticos – que provamos na “Teoria dos Números”…se fez acompanhar por uma ‘análise estatística‘ robusta, e extremamente precisa – realizada ao longo da sequência infinita de…’nºs primos’, uma verdadeiro façanha que nos manteve ocupados por cerca de três anos. O fato da explicação da conjectura de Riemann vir da física (mecânica estatística)…e, as surpreendentes conexões desse campo…com um tema genuinamente matemático, como a ‘teoria dos números’ – revela também a grande unidade do conhecimento científico – bem como…aumenta nosso espanto…diante de um fato tão profundo”. Matemáticos e físicos poderão se “deleitar” com este trabalho…mas suas maiores implicações, provavelmente ficarão por conta da ‘filosofia da ciência’. (texto base)











CurtirCurtir